중심극한정리(Central Limit Theorem, CLT)
모평균 $\mu$, 분산 $\sigma^{2}$의 모집단에서 크기 $n$의 표본을 추출하여 그 표본 평균을 $X$라 할 때, 표본의 크기가 커질수록 $X$의 확률 분포는 모집단의 분포 모양과는 관계없이 평균이 $\mu$, 분산이 $\frac{\sigma^{2}}{n}$인 정규분포에 가까워지는 것을 중심 극한 정리(Central Limit Theorem, CLT)하고 합니다.
따라서 다음과 같은 특징이 있습니다.
- 표본으로 부터 계산된 표본 평균의 평균은 모집단의 평균과 동일하다.
- 계산된 표본 평균들의 산포는 모집단의 산포보다 작아진다.
- 표본평균들의 산포는 표본의 크기에 따라 달라진다.
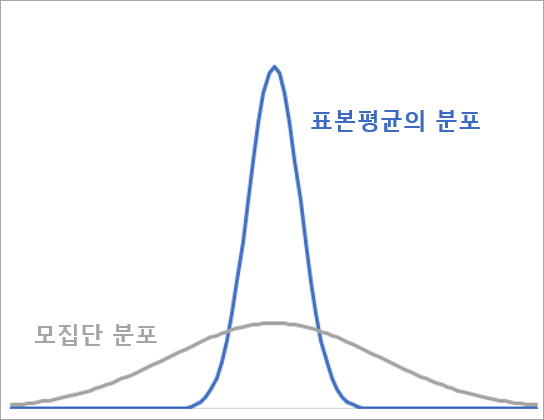
예를 들어, 전국의 초등학교 5학년의 몸무게의 평균값을 표본조사로 알아본다고 가정해봅시다. 모집단의 분포는 명확하지 않지만 표본으로 추출한 $n$명의 표본 평균 분포는 $n$이 클 때 정규분포에 가까워집니다. 이 평균값은 전국 초등학교 5학년의 평균값(모평균 $\mu$)과 동일하고, 분산은 모분산 $\sigma^{2}$를 $n$으로 나눈 값이 됩니다. 이것이 중심 극한 정리입니다.
큰 수의 법칙(또는 대수의 법칙)(Law of Large Numbers, LLN)
중심극한정리에서 알 수 있듯이 표본의 크기, $n$를 키워가면 표본 평균 $X$의 분산은 작아집니다.
즉, 확률 밀도가 모평균 $\mu$의 주위에 높아져 갑니다. 단적으로 말하면 표본 평균은 표본의 크기 $n$이 충분히 커지면 모평균 $\mu$에 한없이 가까워집니다. 이것을 큰 수의 법칙(Law of Large Numbers, LLN)이라 합니다.
모집단을 잘 파악하기 위해서는 되도록 큰 표본을 추출하는 것이 좋다는 것을 의미합니다.
예를 들어, 앞면과 뒷면이 있는 동전 던지기의 경우 앞면이 나올 확률은 1/2이고 뒷면이 나올 확률도 마찬가지로 1/2입니다.

동전 던지기를 2회 하였을 경우를 생각해봅시다. 앞면이 1회, 뒷면이 1회 나올 수도 있겠지만 앞면만 2회, 또는 뒷면만 2회가 나올 수 도 있습니다. 하지만 동전 던지기 횟수를 10회, 1,000회, 1,000,000회처럼 반복 횟수를 무수히 늘려보면 앞면과 뒷면이 나올 확률은 1/2에 가까워진다는 것이 큰 수의 법칙의 예가 될 것입니다.
'유용한 정보들 > 6 시그마(Six Sigma)' 카테고리의 다른 글
| 일원배치 분산분석(ANOVA 분석) 개념 정리 (5) | 2020.10.26 |
|---|---|
| 통계적 가설 검증 방법 (0) | 2020.10.18 |
| 정규 분포 - 연속형 확률 변수의 분포 (0) | 2020.10.11 |
| 6 시그마(Six Sigma) 문제 해결 프로세스 DMAIC (0) | 2020.09.28 |
| 통계학의 기본 개념과 통계학의 기본 용어 정리 (0) | 2020.09.14 |



