정규분포(Normal Distribution)는 다음과 같이 정의되는 확률 분포(Probability Distribution)입니다.
$$f(x) = \frac{1}{\sqrt{2\pi}\sigma }e^{-\frac{(x-\mu )^{2}}{2\sigma ^2}}, -∞<x<∞$$
여기서, π는 원주율(3.14159)을, $e$은 자연로그에서 밑인 네이피어 상수를 의미하며 근삿값은 2.71828인 실수입니다.
$f(x)$는 확률 밀도 함수(Probability density function)이라고 부릅니다.
가로축을 $x$로 세로축을 $f(x)$로 하는 그래프는 아래와 같이 좌우 대칭이며 종 모양의 형태를 가지고 있습니다. 이 확률 분포에 따르는 확률 변수의 평균은 $\mu$, 분산은 $σ^{2}$가 됩니다.
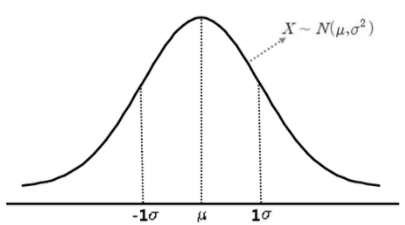
하나의 확률 변수 $X$가 평균은 $\mu$이고 표준편차가 $σ$인 정규분포를 따르는 확률변수이면 이를 기호 $X\sim N(\mu, \sigma^{2})$으로 표현합니다. $N$은 정규 분포의 영어, Normal distribution의 머리글자입니다.
정규분포 식은 복잡하지만 그에 따르는 확률 분포는 대부분 우리에게 익숙한 것들입니다.
예를 들어, 연필 생산 라인에서 생산되는 100그램으로 표시되는 연필에서 측정한 1개의 제품 무게, $X$는 확률 변수가 되지만, 그 확률분포의 확률 밀도 함수는 정규분포가 됩니다.
또 다른 예로 전국의 초등학생 4학년생 중 100명을 무작위로 선정하여 평균 키를 측정하였을 경우 무작위로 선정한 100명의 평균 키, $X$는 다르지만 그 확률 밀도 함수는 정규 분포가 됩니다.
정규 분포 곡선은 몇 가지 중요한 성질을 가지고 있습니다.
첫째, 평균을 중심으로 좌우 대칭입니다. - (symmetric)
둘째, 종 모양입니다. - (Bell shaped)
셋째, 봉우리가 하나입니다. - (Single peaked)
정규 분포 곡선은 평균과 표준편차에 의해서 중심과 퍼짐의 정도가 다르지만 그 전반적인 모양은 변하지 않습니다.
확률 밀도 함수에서 어느 구간에 확률 현상이 일어날 확률은 그 구간에서 확률 밀도 함수와 가로축으로 둘러싸인 부분의 면적으로 나타낼 수 있습니다.
아래 그림과 같이 $\mu ± \sigma$의 구간에서 확률 현상이 일어날 확률, $P(\mu-\sigma ≤ X ≤ \mu + \sigma)$는 68.3%이며, $\mu ± 2\sigma$의 구간에서는 95.4%의 확률이 됩니다.
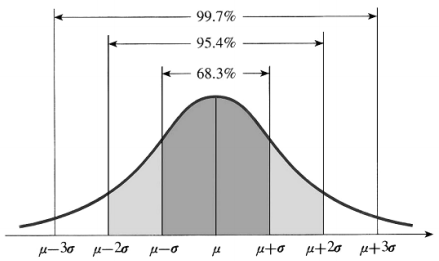
정규 분포에서 평균이 0이고 표준편차가 1이 되는 정규 분포를 표준 정규 분포(Standard Normal distribution)라고 합니다.
확률 변수 $Z$가 표준 정규 분포를 따를 때, 이를 $Z\sim N(0, 1)$로 표시하며 표준 정규 분포의 확률 밀도 함수는 다음과 같습니다.
$$f(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{z^{2}}{2}}, -∞<z<∞$$
통계학 및 6 시그마에서는 평균값을 중심으로 95%의 범위를 자주 사용하는데 아래 그림과 같이 $\mu ± 1.96\sigma$의 경계점을 정규 분포의 양측 5% 점이라 합니다.
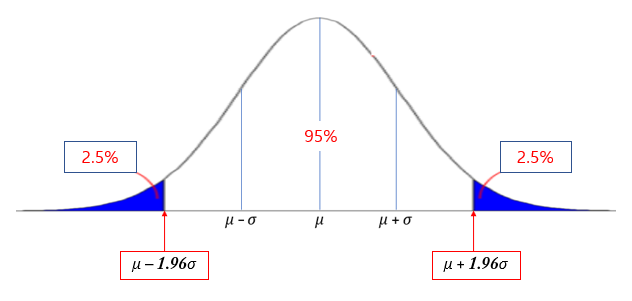
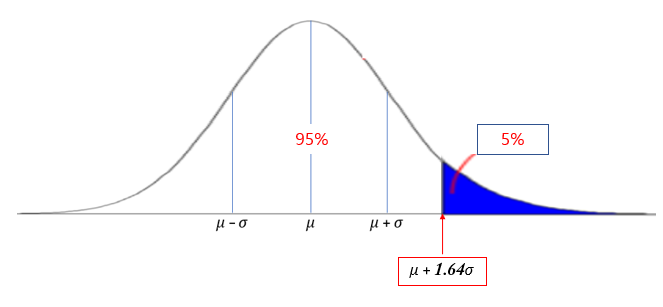
규격 상한, 하한이 있으면 위의 양측 5% 점을 이용할 수 있지만 규격이 상한만 존재할 경우에는 왼쪽에서 오른쪽으로 걸친 95%의 범위를 사용할 수 있습니다. 이들 경계점은 $\mu + 1.64\sigma$에 위치하며 정규 분포의 상위 5%점이라고 합니다.
'유용한 정보들 > 6 시그마(Six Sigma)' 카테고리의 다른 글
| 통계적 가설 검증 방법 (0) | 2020.10.18 |
|---|---|
| 중심 극한 정리와 큰 수의 법칙(대수의 법칙) (0) | 2020.10.13 |
| 6 시그마(Six Sigma) 문제 해결 프로세스 DMAIC (0) | 2020.09.28 |
| 통계학의 기본 개념과 통계학의 기본 용어 정리 (0) | 2020.09.14 |
| 6 시그마와 3.4 ppm의 통계적 의미 (2) | 2020.08.12 |



