실험 등 통계분석에서 중요한 역할을 하는 것이 분산분석입니다.
분산분석(Analysis of variance)이란 특성치의 산포를 제곱합(sum of squares)으로 나타내고 이 제곱합을 실험과 관련된 요인마다 제곱합으로 분해하여 오차보다 특히 큰 영향을 주는 요인이 무엇인가를 찾아내는 분석 방법입니다.
다시 말해, 특성치의 산포를 요인별로 분해하여 어느 요인이 큰 산포를 나타내고 있는가를 규명하는 방법입니다.
분산분석(Analysis of variance)의 이해를 위해서 일원 배치법에서 분산 분석표를 구하는 방법을 따라 해 보면서 분산분석을 자세히 알아봅시다.
참고로 일원 배치법(One-way factorial design)은 어떤 관심 있는 특성치에 대하여 하나의 인자(factor)의 영향을 조사하기 위해 사용하는 가장 단순한 실험 계획법입니다.
예를 들어, 플라스틱을 만드는 회사에서 3가지 반응 온도(50℃, 60℃, 70℃)에 따라 플라스틱의 강도에 영향을 주는지 알아보기 위해 다음과 같이 5회 반복 실험을 하여 결과를 얻었습니다.
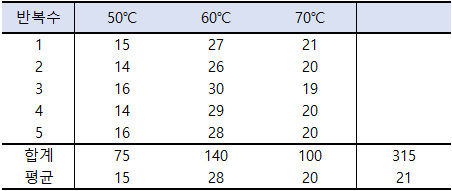
실험 결과를 보면 반응 온도가 60℃에서 플라스틱의 평균 강도가 28로 가장 강한 것을 알 수 있습니다.
이때의 결론은 '반응 온도 60℃가 플라스틱 강도에 가장 효과가 좋다' 아니면 '이것은 단지 우연의 효과이다'처럼 둘 중의 하나의 결론을 내릴 수 있을 것입니다.
이와 같은 실험 데이터가 '우연인가', '우연이 아닌가'에 대한 통계적인 결론을 끌어내는 것이 분산분석의 핵심 내용입니다.
데이터의 분해하기
개별 데이터와 전체 평균의 총편차는 다음과 같이 그룹 간 편차와 그룹 내 편차로 분해가 가능합니다.
(개별 데이터 - 전체 평균) = 그룹 간 편차 + 그룹 내 편차
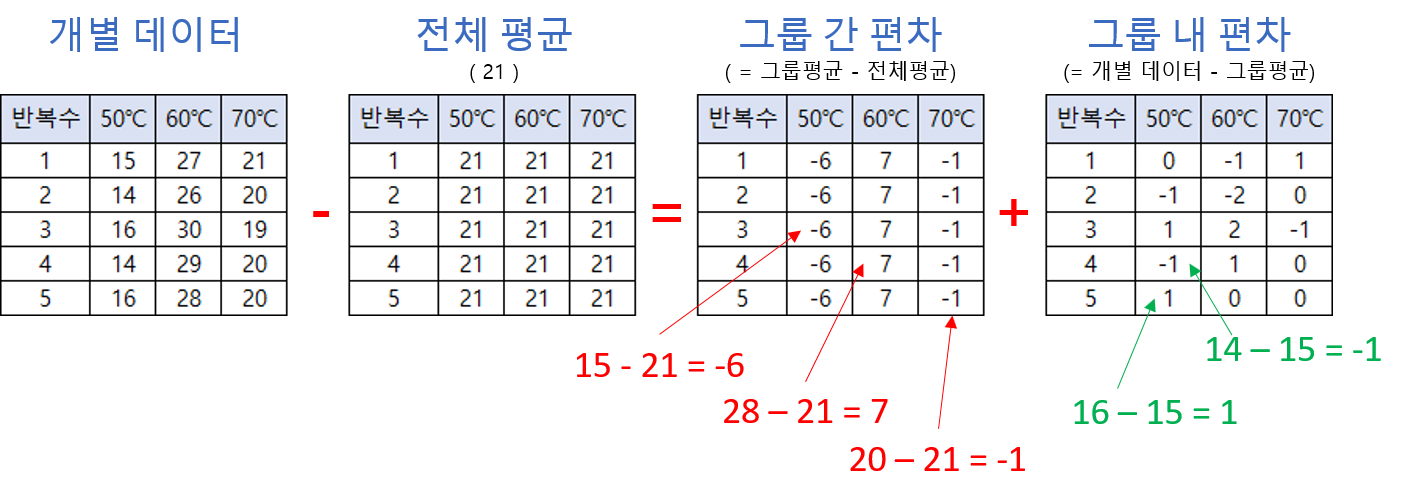
일반화하여 수식으로 표현하면 다음과 같습니다.

그룹 간 편차란 그룹 평균값에서 전체 평균값을 뺀 값입니다.
그룹 내 편차는 개별 데이터에서 그룹 평균값을 뺀 값으로 잔차(residual)라고 부르기도 합니다.
분산분석에서 중요한 것은 그룹 간 편차와 그룹 내 편차입니다.
그룹 간 편차는 그룹 평균의 분산을 나타내므로 그룹 간 차이의 효과는 일반적으로 요인(또는 수준) 차이의 효과를 의미합니다. 그룹 내 편차는 동일 조건하에서 데이터의 분산을 나타내므로 우연의 통계 오차를 나타낸다고 생각할 수 있습니다.
따라서 그룹 간 편차가 그룹 내 편차보다 전체적으로 크면 요인의 차이에 의한 효과가 있다고 볼 수 있으면 반대의 경우에는 요인 차이에 의한 효과는 우연의 통계 오차에 묻히게 되는 것입니다.
(개별 데이터 - 전체 평균) = 그룹 간 편차 + 그룹 내 편차의 관계에서 양변을 제곱하여 각 요인별 변동을 구할 수 있습니다.
다시 말해서, 데이터의 총 변동( 또는 총 제곱합)은 인자 수준의 변화에 의한 변동(그룹 간 변동)과 그룹 내의 오차 변동(또는 잔차 변동)이라는 두 개의 요인으로 분해됩니다.
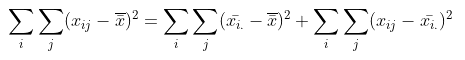
위의 반응 온도에 따른 플라스틱 강도 실험 결과를 위의 식에 따라 계산해보면 좌변 총 변동(total variation)은 446이고 우변의 첫 번째 항, 그룹 간 변동(variation between group)은 430이고 우변의 두 번째 항, 그룹 내 변동(variation within group)은 16이 됩니다.
데이터가 갖는 자유도 계산하기
아래 그룹 간 편차 테이블에서 이들의 값은 그룹 간 편차의 집합이므로 동일 실험의 집합 내 값을 모두 더하면 '0'이 됩니다.
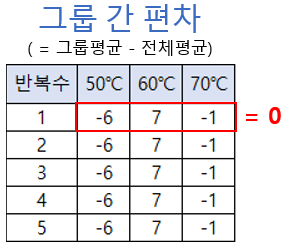
여기에서 2개의 데이터는 자유롭게 움직일 수 있는 값이 될 수 있지만 남은 하나는 전체 합을 0으로 만들어야 하므로 자유로울 수가 없습니다.
따라서 그룹 간 편차의 자유도는 2가 됩니다. 일반적으로 그룹 수에서 '1'을 빼 것이 그룹 간 편차의 자유도가 됩니다.
다음은 그룹 내 편차 테이블에서 3가지 반응 온도(50℃, 60℃, 70℃) 그룹은 각각 5개의 데이터로 구성되고 각 그룹 내의 편차로 만들어지기 때문에 그룹마다 모두 더하면 '0'이 됩니다.
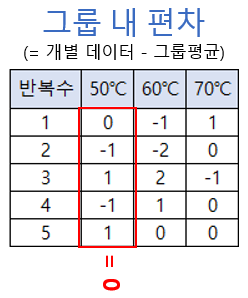
따라서 그룹별로 자유롭게 움직일 수 있는 것은 4가 되고 그룹 내 편차 전체에서 자유롭게 움직일 수 있는 수치는 12개가 됩니다.
그래서 그룹 내 편차의 자유도는 12가 됩니다. 일반적으로 그룹 수 * ( 그룹 내 데이터 수 - 1)이 그룹 내 편차의 자유도가 됩니다.
평균 제곱(분산) 및 검정 통계량 구하기
평균 제곱은 제곱합(변동)을 해당 자유도로 나누면 됩니다.
따라서, 그룹 간 편차의 평균 제곱은 그룹 간 변동(430)을 그룹 간 편차의 자유도(2)로 나누면 215가 됩니다.
마찬가지로 그룹 내 편차의 평균 제곱은 그룹 내 변동(16)을 그룹 내 편차의 자유도(12)로 나누면 1.33이 됩니다.
검정 통계량 F는 그룹 간 편차의 평균 제곱과 그룹 내 편차의 평균 제곱의 비로써 F 검정에 사용합니다.
그룹 간 편차의 평균 제곱(215)을 그룹 내 편차의 평균 제곱(1.33)으로 나누면 161.25가 됩니다.
분산 분석표(ANOVA Table) 작성하기
지금까지 도출한 결과를 이용하여 일원 배치 분산 분석표는 작성해 보면 다음과 같습니다.

분산 분석표 작성이 되었으면 마지막 단계로 가설검정을 실시하여 봅시다.
귀무가설 : 반응 온도의 차이는 플라스틱 강도에 효과가 없다. (H0)
대립가설 : 반응 온도의 차이는 플라스틱 강도에 효과가 있다. (H1)
유의 수준(α)은 5%로 사전 합의
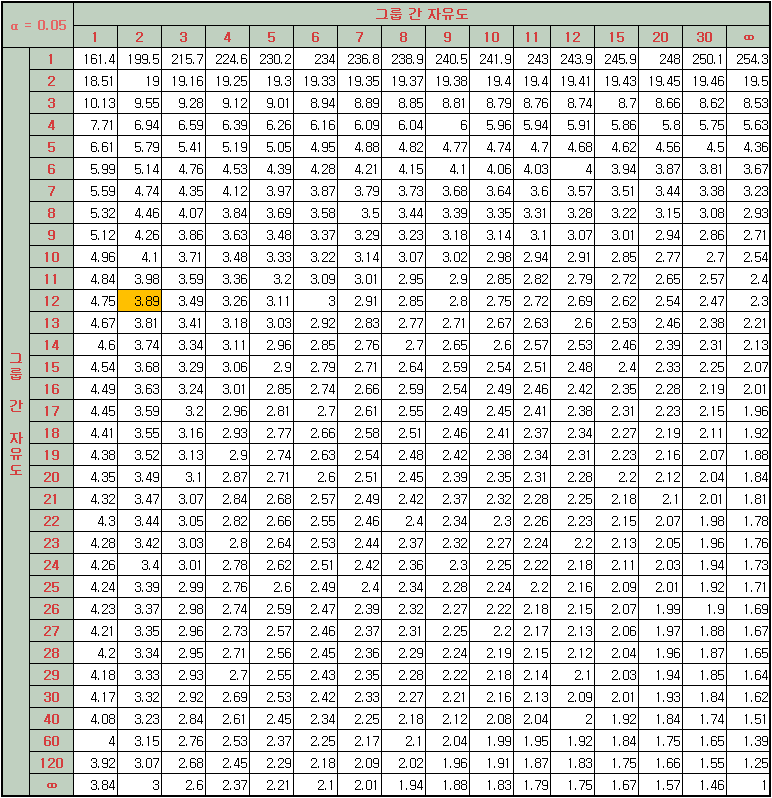
F 검정을 위해 아래의 F 분포표(α = 0.05)에서 그룹 간 편차의 자유도는 2이고 그룹 내 자유도는 12인 F0를 찾아보면 3.89입니다. 즉 유의 수준이 5% 일 때 검정 통계량 F-값 ≥ 3.89 이면 귀무가설(H0)은 기각됩니다.
따라서 요인(반응 온도)은 특성치(플라스틱의 강도)에 영향을 미친다고 할 수 있으며 요인의 수준 간에 유의한 차이가 있다 것으로 결론을 내릴 수 있습니다.
분산 분석표를 만들기 위해 값들을 하나씩 채워가면서 F-검정을 통해 요인이 특성치에 영향이 있는지 요인의 수준 간에 유의한 차이가 있는지 알아보았습니다.
'유용한 정보들 > 6 시그마(Six Sigma)' 카테고리의 다른 글
| [통계학 기초] 표준 정규분포(Standard Normal Distribution) (0) | 2020.11.03 |
|---|---|
| 실험 계획법(DOE)과 5가지 기본 원리 (0) | 2020.10.31 |
| 통계적 가설 검증 방법 (0) | 2020.10.18 |
| 중심 극한 정리와 큰 수의 법칙(대수의 법칙) (0) | 2020.10.13 |
| 정규 분포 - 연속형 확률 변수의 분포 (0) | 2020.10.11 |



