파레토 법칙(Pareto Principle), 80대 20 법칙

파레토 법칙(Pareto Principle)은 전체 결과의 80%가 20%의 소수의 원인에 의해서 결정되는 현상을 나타내는 법칙이며 80/20 법칙, 8대 2의 법칙 또는 인자 희소성의 원칙(Principle of factor sparsity)이라고도 합니다.
파레토 법칙은 이탈리아 경제학자 빌프레도 파레토(Vilfredo Pareto, 1848~1923)가 1896년 논문에서 소득 분포에 대하여 발표한 통계적 법칙으로 '이탈리아 전체 인구의 20%가 이탈리아 전체 부의 80%를 가지고 있다'는 주장에서 유래되었고 여러 경제학자들에 의해서 파레토 법칙으로 발전하였습니다.
파레토 법칙은 이후 경제, 사회, 제조 등의 다양한 분야에서 확인되고 증명되었을 뿐만 아니라 우리의 일살 생활에서도 흔히 경험해 볼 수 있는 법칙입니다.
파레토 법칙은 다음의 사례처럼 다양한 분양에서 현실적으로 잘 들어맞는 법칙입니다.
☞ 불량을 일으키는 결함의 80%는 상위 20%의 결함에 의해서 발생한다.
☞ 프로 야구팀의 전체 연봉의 80%는 상위 연봉자 20% 인원의 연봉이다.
☞ 최근 통화 목록의 80%는 20%의 인원에게 집중되어 있다.
☞ 등록된 주식의 시가 총액의 80%는 상위 20개 종목의 시가 총액과 비슷하다.
☞ 상점의 진열된 상품 중 매출의 80%을 차지하는 것은 잘 파리는 20%의 상품이다.
☞ 백화점, 모바일 게임 등의 매출의 80%는 20%의 고객에 의해서 발생한다.
☞ 스마트 폰에 설치된 어플 중 사용시간의 80%는 20% 내의 어플이다.
여기서 말하는 80%와 20%는 절대적인 수치를 의미하는 것이 아니라 사회적 현상을 설명할 때 크고 작은 것을 상징하는 것으로 이해하면 될 것입니다.
실제 산업 전반에 걸쳐 품질 개선 업무를 하는 실무에서는 전체 불량을 모두 개선하는 것이 아니라 파레토 차트(불량률이 높은 것부터 가로축에 나열하고 누적 불량률을 계산하여 같이 표현)를 그려서 상위 20% 불량 개선에 자원을 집중하고 80%의 개선 효과를 기대할 수 있습니다.
이처럼 파레토 법칙은 우리의 일상생활에서 다양한 상황이 존재할 경우 선택과 집중을 할 수 있는 근거를 만들어 줍니다. 따라서 한정된 시간과 자원을 활용하여 최대의 효과를 만들기 위해서는 선택과 집중은 반드시 필요합니다.
파레토 법칙은 상위 20%에 집중하기 때문에 다양성이 존중되고 있는 최근 떠오르고 있는 분야들에서는 한계점을 가지고 있습니다. 지금 당장은 80%의 효과를 기대할 수 있는 20%에 집중하는 것이 효율적일 수 있겠지만 다양성에서 의도치 않게 혁신적인 아이템이 발굴되는 사례가 많이 있습니다. 대표적인 살례가 직원들이 재미 삼아 만든 Google Map, 크리스마스에 시간을 보내기 위해 만든 파이썬(Python) 등이 있습니다.
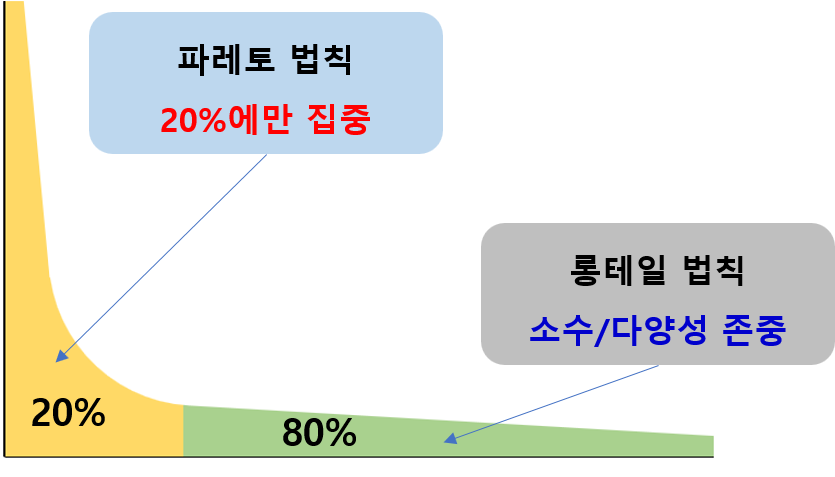
최근 2004년부터 파레토 법칙과 상반되는 내용의 롱테일 법칙(Long Tail Law)에 많은 관심이 집중되고 있습니다.
롱테일 법칙은 미국의 인터넷 비즈니스 관련 잡지 와이어드(Wired)의 편집장인 크리스 앤더스(Chris Anderson)가 "주목받지 않는 대다수의 사람들이 VIP와 같은 핵심적인 소수보다 더 큰 이익이나 가치를 창출하는 현상"을 설명하면서 사용한 표현이 롱테일(Long tail)입니다.
시장 경쟁이 치열해지고 인터넷 상거래, 인터넷 쇼핑몰과 같은 온라인 판매가 증가되면서 평범하였던 80%의 중요성이 부각되고 있습니다.
롱테일 법칙의 효용성을 잘 드러나는 대표적인 사례가 아마존의 도서 판매입니다. 사업 초창기 온라인 서점이 주력이었던 아마존 닷컴의 전체 수익의 절반 이상이 오프라인 서점에서는 실적이 부진하였던 비인기 도서들에서 창출되었다고 합니다.
이처럼 롱테일 법칙은 마케팅 등에 한정적인 분야에서는 파레토 법칙을 뒤엎는 효용성을 보이고 있습니다.
'유용한 정보들' 카테고리의 다른 글
| [베타 키우기] 베타 어항 히터 설치하기 (0) | 2020.10.15 |
|---|---|
| CPU, GPU, GPGPU의 차이 (0) | 2020.09.08 |
| [베타 키우기] 베타 키우기 초보 입문 (3) | 2020.08.29 |
| 텍스트 에디터 지니(Geany) 사용 방법 (0) | 2020.08.29 |
| 윈도우 단축키를 알면 힘이 된다 (0) | 2020.07.19 |



